排列組合問題,考察的側重點在於理解,而非計算,所以對於一些基本概念,比如加法原理、乘法原理要理解透徹。排列組合題型變化多樣,經典題型和方法很多,要求大家逐一掌握,熟練應用。首先回顧一下基本概念和基本公式:
逆向公式:滿足條件的情況數=總情況數-不滿足條件的情況數
那麼對於常考的題型,逐一進行講解:
題型一:基礎公式型:
【例1】(10-國考-48)一公司銷售部有4名區域銷售經理,每人負責的區域數相同,每個區域都正好有兩名銷售經理負責,而任意兩名銷售經理負責的區域隻有一個相同。問這4名銷售經理總共負責多少個區域的業務?
A.4 B.6
C.8 D.12
【答案】B。
【解析】本題屬於排列組合題型,本題的難點在於比較抽象,每個區域都是由兩名銷售經理負責,而不同區域的銷售經理必須是不同的組合(因為如果是相同的組合的話,就違背了“任意兩名銷售經理負責的區域隻有一個相同”),從4名區域銷售經理當中一共可以挑出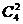 =6(個)不同的組合,恰好對應了滿足題意的六個區域。
=6(個)不同的組合,恰好對應了滿足題意的六個區域。
題型二:分類討論型:
【例2】(11-國考-72)甲、乙兩個科室各有4名職員,且都是男女各半。現從兩個科室中選出4人參加培訓,要求女職員比重不得低於一半,且每個科室至少選一人。問有多少種不同的選法?
A. 67 B. 63
C. 53 D. 51
【答案】D。
【解析】本題屬於排列組合題型,滿足條件的情況可以分幾種:
第一種情況:2男2女: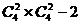 =34(排除4名職員來至同一個部門的情況)
=34(排除4名職員來至同一個部門的情況)
第三種情況:0男4女:1
所有情況數等於34+16+1=51種,答案為D。
| 下一頁 |

 分享到人人
分享到人人 分享到QQ空間
分享到QQ空間
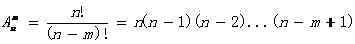
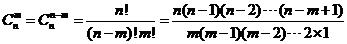











 恭喜你,發表成功!
恭喜你,發表成功!

 !
!





















