排列组合问题,考察的侧重点在于理解,而非计算,所以对于一些基本概念,比如加法原理、乘法原理要理解透彻。排列组合题型变化多样,经典题型和方法很多,要求大家逐一掌握,熟练应用。首先回顾一下基本概念和基本公式:
逆向公式:满足条件的情况数=总情况数-不满足条件的情况数
那么对于常考的题型,逐一进行讲解:
题型一:基础公式型:
【例1】(10-国考-48)一公司销售部有4名区域销售经理,每人负责的区域数相同,每个区域都正好有两名销售经理负责,而任意两名销售经理负责的区域只有一个相同。问这4名销售经理总共负责多少个区域的业务?
A.4 B.6
C.8 D.12
【答案】B。
【解析】本题属于排列组合题型,本题的难点在于比较抽象,每个区域都是由两名销售经理负责,而不同区域的销售经理必须是不同的组合(因为如果是相同的组合的话,就违背了“任意两名销售经理负责的区域只有一个相同”),从4名区域销售经理当中一共可以挑出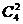 =6(个)不同的组合,恰好对应了满足题意的六个区域。
=6(个)不同的组合,恰好对应了满足题意的六个区域。
题型二:分类讨论型:
【例2】(11-国考-72)甲、乙两个科室各有4名职员,且都是男女各半。现从两个科室中选出4人参加培训,要求女职员比重不得低于一半,且每个科室至少选一人。问有多少种不同的选法?
A. 67 B. 63
C. 53 D. 51
【答案】D。
【解析】本题属于排列组合题型,满足条件的情况可以分几种:
第一种情况:2男2女: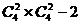 =34(排除4名职员来至同一个部门的情况)
=34(排除4名职员来至同一个部门的情况)
第三种情况:0男4女:1
所有情况数等于34+16+1=51种,答案为D。
| 下一页 |

 分享到人人
分享到人人 分享到QQ空间
分享到QQ空间
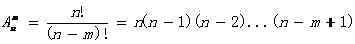
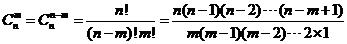











 恭喜你,发表成功!
恭喜你,发表成功!

 !
!





















