2014云南省考：列表法解决朴素逻辑问题

朴素逻辑是自发的无序的思维的过程，对于朴素逻辑累的题目我们一般使用列表法、假设法、带入排除法等方法来解决，今天为大家介绍列表法。

例一：

甲、乙、丙三朋友去参观车展，看到一款轿车。甲说：“这不是奇瑞，也不是荣威。”乙说：“这不是奇瑞，而是红旗。丙说：“这不是红旗，而是奇瑞。”后来，车展管理员说：“三个人，有一个人的两个判断都对；另一个的两个判断都错；第三个人的两个判断一对一错。”

由此可知：

A.这辆轿车是奇瑞轿车

B.这辆轿车是荣威轿车

C.这辆轿车是红旗轿车

D.上面三辆轿车都不是

解析：

遇到这样几个人讨论，每个人对部分的内容进行猜测的题，我们就可以用列表法。根据题意，可得：

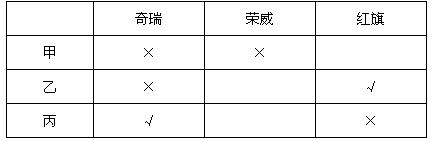
根据图表，我们可以直观的看出，乙、丙所说的话是矛盾，集合题干可得，乙和丙必然一个两个都对，一个两个都错，那么甲必然是两个判断一对一错。接下来我们要结合假设法进一步做题。

1.我们假设甲的前半句是对的，后半句是错的，则这辆车不是奇瑞，是荣威。那么下面乙、丙两句话就应该是乙两句都对，丙两句都错，从乙两句都对可得，车不是奇瑞，而是红旗，此时，甲、乙矛盾，所以第一种假设错误。

2.我们假设甲的前半句是错的，后半句是对的，则该车是奇瑞，不是荣威。丙的两句都对，该车是奇瑞、不是红旗。乙的两句都错，该车应该是奇瑞，不是红旗，与题干吻合。所以正确答案应为，该车是奇瑞。

所以选A。

例二：

有红、蓝、黄、白、紫五种颜色的皮球，分别装在五个盒子里。甲、乙、丙、丁、戊五人猜测盒子里皮球的颜色。甲：第二盒是紫的，第三盒是黄的。乙：第二盒是蓝的，第四盒是红的。丙：第一盒是红的，第五盒是白的。丁：第三盒是蓝的，第四盒是白的。戊：第二盒是黄的，第五盒是紫的。猜完之后打开盒子发现，每人都只猜对了一种，并且每盒都有一个人猜对。

由此可以推断：

A.第一个盒子内的皮球是蓝色的

B.第三个盒子内的皮球不是黄色的

C.第四个盒子内的皮球是白色的

D.第五个盒子内的皮球是红色的

解析：

根据题意，可画表：

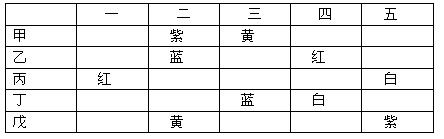
列完表之后，我们先观察，找特殊，从特殊入手做题。根据题目，每个纵向和横向，都有且仅有一个是正确的。从图表上看，第一个盒子里一定是红的，因为每个盒子都有人猜对。所以乙才的四里面是红的是错的，第二个盒子里应该是蓝的。既然第二个里面应该是蓝的，所以第二个盒子里不能是紫的和黄的。所以第三个应该是黄的第五个应该是紫的。第四个应该是白的。最后得出答案应该是C。

用列表法解决朴素逻辑问题，关键是列好表不要急着下笔，而是要找特殊，从特殊为切入口，解决问题。

来源：中公教育