中国学生做SAT数学题有两大障碍

在SAT考试中对于美国学生比较难的数学问题对于中国学生来说是通常是比较容易的，毫无疑问是中国学生的优势所在。但在日常教学中发现中国学生在SAT数学题上通常遇到两大障碍。

障碍一：由于对英语数学词汇和表达不熟悉，造成题目理解的困难或错误。

比如2013年一套SAT数学部分题目，不少同学感到有些困惑。题目如下：

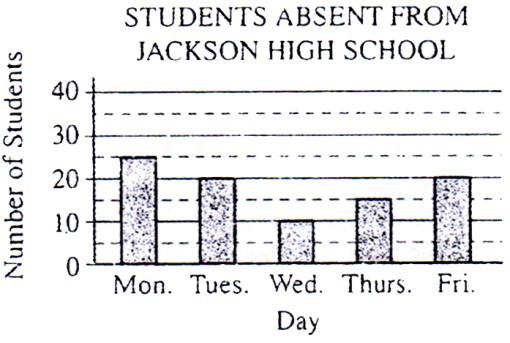
The bar graph above shows the number of students who were absent from Jackson High School each day last week. Of those students, 8 were absent exactly 2 days each, 1 was absent 3 days, and no students were absent more than 3 days. If 5 percent of the students in the school were absent at least 1 day last week, how many students are enrolled in Jackson High School?

我们将之翻译成中文：

以上图形说明了杰克逊高中上周每一天的学生缺勤情况。在缺勤的学生中，有8名学生缺勤两天，1名学生缺勤三天，没有一位学生缺勤超过三天。假如该校学生上周有5%至少缺勤一天，请问杰克逊高中在校学生是多少？

这是一道结合了图形理解和人次及实际人数的计算，对于学生的英语数学题正确理解及计算中的准确性有一定的要求。

根据图形提供的信息，上周，该中学缺勤的人次总共是25+20+10+15+20=90，8名学生缺勤两天，则8人造成16人次缺勤，1名学生缺勤三天，则1人造成3人次缺勤。由此，90人次缺勤中实际缺勤一次及以上的人数为90-8-2=80。原题信息5%的学生至少缺勤一天，则学校总人数是80除以5%，全校人数1600人。

障碍二：SAT数学题多需要巧妙的思维，而非复杂的运算。

在与中国SAT学生交流的过程中，我们经常会说“SAT数学题是脑筋急转弯”，意思就是题目经常需要学生有巧妙的思维，而不见得是复杂的计算能力。

以下是一道经典的老题：

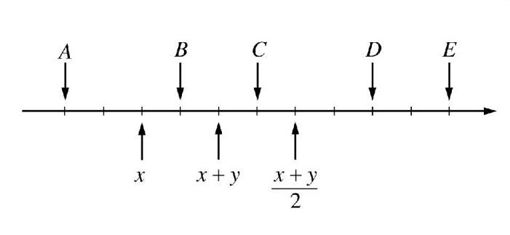
On the number line above, the tick marks are equally spaced. Which of the lettered points (A,B,C,D and E) represents y ?

以上数据线，各个小竖线所切分部分为等长，请问哪一个点代表y?

不少同学因为x+y处于x和(x+y)/2之间而困惑不解，甚至认为原题图形有错。惯性思维促使同学们总觉得(x+y)/2应该小于(x+y)呀，于是大家不知如何下手。其实(x+y)/2在哪里根本不影响本题，只要记住(x+y)/2一定在x点和y点之间，加上所有小竖线划分的区间等值，就可以判定y点就是E。

当然我们可以进行相对复杂的运算，由于(x+y)在x和(x+y)/2之间，我们可以列出以下等式：(x+y)X2=x+(x+y)/2 可以推导出x= -3 y

举例，y=1, x= - 3 应该符合这一条件。由此，x点为- 3, x+y为 -2，(x+y)/2 为 -1, y点应该是1。由此推断小竖线划分的每一个小格为0.5，由此推出y点在E。这当然是比较复杂的做法，虽然可以得出同样的结论，但花费的时间更多，过程更为复杂，复杂过程造成差错的可能性也就增加了。

再例如此题：

In the xy-coordinate plane, point P is the reflection of the point with coordinates (3, 1) across the line y = x. Point T is the reflection of point P across the y-axis. What are the coordinates of T?

(A) (–3, 1)

(B) (–1, –3)

(C) (–1, 3)

(D) (1, –3)

(E) (3, –1)

题目翻译成中文：在由x轴和y轴形成的平面上，点P是座标为(3,1)的点基于轴y=x的映射点，点T是点P基于y轴的映射点，问：点T的座标？

这道题目有聪明且快捷的做法吗？轴y=x是以45度角斜穿xy平面的直线，且经过原点(0,0)，点(3,1)基于轴y=x映射到点P，则点P的座标应该与(3,1)一样，x,y值同为正值。点T是点P基于y轴的映射，则T点与P点的y座标相同，x座标为负值。由此答案应该是座标中x值为负值，y值为正值。满足这一条件的只有A和C。简单画一个图形就知道，A点是(3,1)基于y轴的映射点，应该只有C点满足要求。

假如我们通过几何图形的计算，比如P点，原点和(3,1)形成等腰三角形，且y=x这一直线与P点与(3,1)形成的三角形的底形成直角，这样进行一番计算……我只能说，同学们，当你拿起草稿纸，开始大张旗鼓地计算的话，你基本上已经走上了一条错误的道路。

SAT考试专家郑峻华说，相对而言SAT数学题的知识难度对于中国学生并不高，关键在于熟悉数学的英语词汇和表达，多用灵活的思路，经过系统的学习和练习，都完全可以拿到很高的分数。2016新版样题显示出SAT数学题目的文字部分长度大于现版，对中国考生而言，能否正确理解题目的要求是一个考验，数学部分更侧重考察推理和应用能力。学生在备考中，基础的数学词汇需要记忆，熟悉各类题型、必要的练习自然是不可少的。同时切记不要粗心，在数学上犯无谓的错误造成失分实在可惜。

来源：西奈山教育