2013年浙江省考：數學運算中的集合容斥問題

數學運算中的集合問題，也稱容斥原理是近幾年經常出現的題型，考生應將其作為典型題目加以掌握。解決容斥原理的題目，方法是關鍵。此類題型主要包括兩集合問題和三集合問題，並且近幾年常出現的容斥問題基本都是涉及三集合的，本篇文章華圖公務員考試研究中心就針對三集合的題目進行匯總。

三集合容斥問題主要有以下三種題型：

1、三集合標准型核心公式

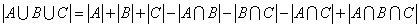
2、三集合圖示標數型（文氏圖或者叫做韋恩圖法）

  a.特別注意“滿足某條件”和“隻滿足某條件”的區別﹔

  b.特別注意有沒有“三個條件都不滿足的情形”﹔

1. 三集合整體重復型核心公式

    三集合容斥問題中，有些條件未知時，就不能直接使用標准型公式，而是運用整體重復型公式同樣可以解答。特別當題目中說明分別滿足一種、兩種、三種條件的個數時，使用整體重復型公式。並且，三集合整體重復型公式是現在國家公務員考試考查三集合容斥問題的重點。另外，可利用尾數法進行快速求解。

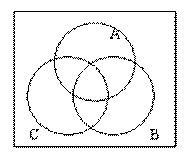
原理：在三集合題型中，假設滿足三個條件的元素數量分別時A、B和C，而至少滿足三個條件之一的元素的總量為W。其中，滿足一個條件的元素數量為x，滿足兩個條件的元素數量為y，滿足三個條件的元素數量為z，根據右圖可以得到下滿兩個等式：

W=x+y+z         

A+B+C=x×1+y×2+z×3

 下面通過幾個例題闡述三集合容斥的相關內容：

【例1】對某單位的100名員工進行調查，結果發現他們喜歡看球賽和電影、戲劇。其中58人喜歡看球賽，38人喜歡看戲劇，52人喜歡看電影，既喜歡看球賽又喜歡看戲劇的有18人，既喜歡看電影又喜歡看戲劇的有16人，三種都喜歡看的有12人，則隻喜歡看電影的有( )。

A.22人        B.28人       C.30人        D.36人

【解析】設A=喜歡看球賽的人58，B=喜歡看戲劇的人38，C=喜歡看電影的人52，則有：

A∩B=既喜歡看球賽的人又喜歡看戲劇的人18

B∩C=既喜歡看電影又喜歡看戲劇的人16

A∩B∩C=三種都喜歡看的人12

A∪B∪C=看球賽和電影、戲劇至少喜歡一種100

由集合運算公式可知：C∩A = A+B+C-(A∪B∪C+A∩B+B∩C-A∩B∩C)

=148-(100+18+16-12)=26

所以，隻喜歡看電影的人=C-B∩C-C∩A+A∩B∩C

=52-16-26+12=22

注：這道題運用公式運算比較復雜，運用文氏圖我們很快就可以看出結果。解法如下：

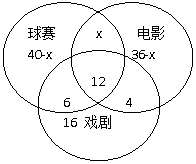
由題意知：（40-x）+x+(36-x)+6+12+4+16=100， 解得 x=14﹔ 則隻喜歡看電影的人有 36-x=22。

【例2】外語學校有英語、法語、日語教師共27人，其中隻能教英語的有8人，隻能教日語的有6人，能教英、日語的有5人，能教法、日語的有3人，能教英、法語的有4人，三種都能教的有2人，則隻能教法語的有( )。

A.4人         B.5人         C.6人        D.7人

解析：首先採用公式法解決此題，設A=英語教師8+5+4-2=15，B=法語教師，C=日語教師6+5+3-2=12,(但應注意的是在做題之前，我們首先必須了解公式中A，B,C三個集合所代表的含義，並非A=8,C=6.),則C= A∪B∪C-A-C+A∩B+B∩C+C∩A-A∩B∩C

     =27-15-12+5+3+4-2=10，那麼隻能教法語的教師=10-3-4+2=5

 另外，此題如果用韋恩圖法會相當簡單，設隻能教法語的人數為X,則依題意得韋恩圖(見下圖)：

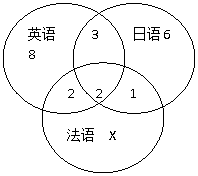
由題意我們有 27=8+3+6+2+2+1+X, 解得X=5。

【例3】某高校對一些學生進行問卷調查。在接受調查的學生中，准備參加注冊會計師考試的有63人，准備參加英語六級考試的有89人，准備參加計算機考試的有47人，三種考試都准備參加的有24人，准備選擇兩種考試都參加的有46人，不參加其中任何一種考試的都15人。問接受調查的學生共有多少人？（   ）

  A.120          B.144            C.177              D.192

【解析】根據題意，分別已知兩種條件、三種條件都滿足的個數，設所有准備參加考試的學生人數為W，隻准備參加一門考試的學生人數為X。使用三集合整體重復型公式：

   W=X+46+24

63+89+47=X+2×46+3×24

 根據尾數法，解得x尾數是5，W尾數是5。因此，學生總數=W+15，尾數為0，選A。

【例4】某市對52種建筑防水卷材產品進行質量抽檢，其中有8種產品的低溫柔度不合格，10種產品的可溶物含量不達標，9種產品的接縫剪切性能不合格，同時兩項不合格的有7種，有1種產品這三項都不合格。則三項全部合格的建筑防水卷材產品有多少種？（）

A. 37      B. 36      C. 35     D. 34

【解析】根據題意，分別已知滿足一種條件、兩種條件的個數，設一項不合格的為X,所有不合格產品為W。使用三集合整體重復型公式：

    W=X+7+1

    8+9+10=X+2×7+3×1

   根據尾數法，解得X尾數為0，W尾數為8。 因此，全合格的產品數=總數-W = 52-W，尾數為4，選D。

 通過以上幾個三集合例題可以發現，對於容斥問題首先判斷題型，是三集合元素已知的題目，還是三集合整體重復型題目。三集合標准型公式和整體重復型公式的適用情況是不同的：標准型公式適用於各項條件都明確給出的情況，而整體重復型公式適用於分別給出滿足一種、兩種、三種條件的個數，因為這三者之間沒有任何包含關系。區分好兩種情形，特別是整體重復型公式，三集合容斥問題就迎刃而解了。華圖公務員考試研究中心祝大家在考試中順利通關！

來源：華圖教育