余數問題中的一個重要問題就是同余問題,在同余問題解決過程中,推薦代入法和口訣法兩大類。其中口訣法是公倍數做周期,余同取余,和同加和,差同減差的應用,但是有時候會出現余不同,和不同並且差也不同的現象,這就需要我們採用剩余定理進行解決。下面就由華圖公務員考試研究中心為大家進行詳細講解。
剩余定理的原理是在“孫子問題”現代數論中的一個一次同余問題,它最早出現在我國公元四世紀的數學著作《孫子算經》中。《孫子算經》卷下“物不知數”題說:有物不知其數,三個一數余二,五個一數余三,七個一數又余二,問該物總數幾何?顯然,這相當於求不定方程組
N=3x+2,N=5y+3,N=7x+2
的正整數解N,或用現代數論符號表示,等價於解下列的一次同余組:
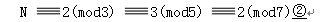
《孫子算經》所給答案是N=23。由於孫子問題數據比較簡單,這個答數通過試算也可以得到。但是《孫子算經》並不是這樣做的。“物不知數”題的術文指出解題的方法:三三數之,取數七十,與余數二相乘﹔五五數之,取數二十一,與余數三相乘﹔七七數之,取數十五,與余數二相乘。將諸乘積相加,然后減去一百零五的倍數。列成算式就是:
N=70×3+21×3+15×2-2×105。
這裡105是模數3、5、7的最小公倍數,容易看出,《孫子算經》給出的是符合條件的最小正整數。對於一般余數的情形,《孫子算經》術文指出,隻要把上述算法中的余數2、3、2分別換成新的余數就行了。以R1、R2、R3表示這些余數,那麼《孫子算經》相當於給出公式
N=70×R1+21×R2+15×R3-P×105(p是整數)。
孫子算法的關鍵,在於70、21和15這三個數的確定。后來流傳的《孫子歌》中所說“七十稀”、“廿一枝”和“正半月”,就是暗指這三個關鍵的數字。《孫子算經》沒有說明這三個數的來歷。實際上,它們具有如下特性:
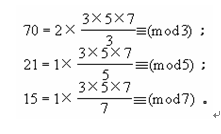
也就是說,這三個數可以從最小公倍數M=3×5×7=105中各約去模數3、5、7后,再分別乘以整數2、1、1而得到。假令k1=2,K2=1,K3=1,那麼整數Ki(i=1,2,3)的選取使所得到的三數70、21、15被相應模數相除的時候余數都是1。由此出發,立即可以推出,在余數是R1、R2、R3的情況下,
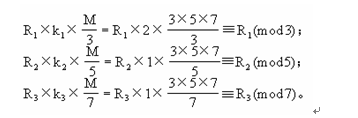
綜合以上三式又可得到
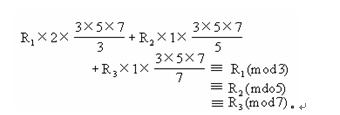
因為M=3×5×7可被它的任一因子整除,於是又有:
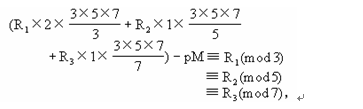
這裡P是整數。這就証明了《孫子算經》的公式。應用上述推理,可以完全類似地把孫子算法推廣到一般情形:設有一數N,分別被兩兩互素的幾個數a1、a2、……an相除得余數R1、R2、……Rn,即
N≡Ri(modai)(i=1、2、……n),
隻需求出一組數Ki,使滿足
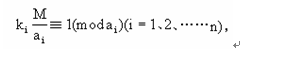
那麼適合已給一次同余組的最小正數解是
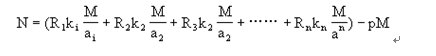
(P是整數,M=a1×a2×……×an),這就是現代數論中著名的剩余定理。如上所說,它的基本形式已經包含在《孫子算經》“物不知數”題的解法之中。不過《孫子算經》沒有明確地表述這個一般的定理。
剩余定理的原理比較繁瑣,不如直接套用解題方法進行快速解題更能解決行測中的類似問題。下面給出一些例題,對剩余定理的解題方法加以熟練:
【例1】一個數被3除余1,被4除余2,被5除余4,這個數最小是多少?
【解析】題中3、4、5三個數兩兩互質。
則〔4,5〕=20﹔〔3,5〕=15﹔〔3,4〕=12﹔〔3,4,5〕=60。
為了使20被3除余1,用20×2=40﹔
使15被4除余1,用15×3=45﹔
使12被5除余1,用12×3=36。
然后,分別乘以他們的余數:40×1+45×2+36×4=274,
因為,274>60,所以,274-60×4=34,就是所求的數。
【例2】一個數被3除余2,被7除余4,被8除余5,這個數最小是多少?
在1000內符合這樣條件的數有幾個?
【解析】題中3、7、8三個數兩兩互質。
則〔7,8〕=56﹔〔3,8〕=24﹔〔3,7〕=21﹔〔3,7,8〕=168。
為了使56被3除余1,用56×2=112﹔
使24被7除余1,用24×5=120﹔
使21被8除余1,用21×5=105﹔
然后,112×2+120×4+105×5=1229。
因為,1229>168,所以,1229-168×7=53,就是所求的數。
再用(1000-53)/168得5, 所以在1000內符合條件的數有5個。
【例3】一個數除以5余4,除以8余3,除以11余2,求滿足條件的最小的自然數。
【解析】題中5、8、11三個數兩兩互質。
則〔8,11〕=88﹔〔5,11〕=55﹔〔5,8〕=40﹔〔5,8,11〕=440。
為了使88被5除余1,用88×2=176﹔
使55被8除余1,用55×7=385﹔
使40被11除余1,用40×8=320。
然后,176×4+385×3+320×2=2499,
因為,2499>440,所以,2499-440×5=299,就是所求的數。
【例4】有一個年級的同學,每9人一排多5人,每7人一排多1人,每5人一排多2人,問這個年級至少有多少人 ?
【解析】題中9、7、5三個數兩兩互質。
則〔7,5〕=35﹔〔9,5〕=45﹔〔9,7〕=63﹔〔9,7,5〕=315。
為了使35被9除余1,用35×8=280﹔
使45被7除余1,用45×5=225﹔
使63被5除余1,用63×2=126。
然后,280×5+225×1+126×2=1877,
因為,1877>315,所以,1877-315×5=302,就是所求的數。
對剩余定理問題進行直接套用的方式是解決此類題目最快的方法,希望考生記住解題步驟,進行相關問題的解決。
來源:華圖教育

 分享到人人
分享到人人 分享到QQ空間
分享到QQ空間






























