5.利潤問題

　　利潤率：

　　折扣率：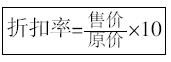

　　部分打折：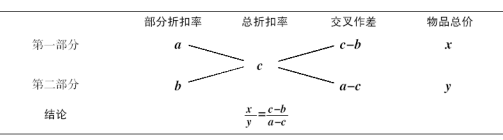

　　6.容斥原理

　　二集合容斥原理：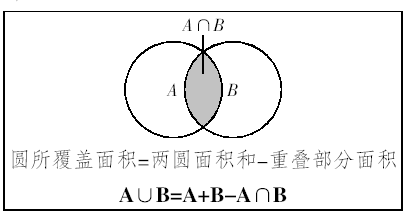

　　三集合容斥原理：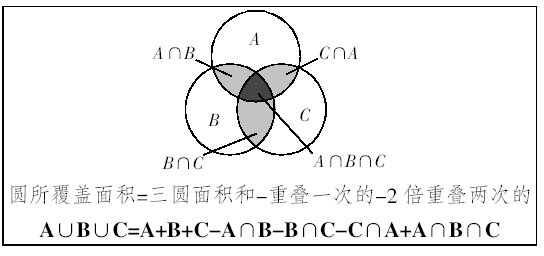

　　7.排列組合

　　排列指的是從n個不同元素中任取m個按照一定的順序排成一列，排列種數記作。根據乘法原理，把整件事分成m步，挑第一個有n種選擇，挑第二個有(n-1)種選擇，以此類推可得：=n×(n-1)×…×(n-m+1) 如果直接對n個不同元素進行排列，就是=n×(n-1)×…×3×2×1=n!，稱之為“全排列”。組合指的是從n個不同元素中取出m個元素作為一組,組合種數記作。根據排列的計算方法,從m個不同元素任取n個排成一列有種情況,每組有種排列,則組合數：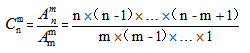

　　環線排列：n個人圍成一圈，不同的排列方式有　=(n-1)!

　　種傳球問題：傳球問題的種類數為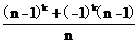

　　n個人經過k次傳球，球回到發球人手上的傳球方式有m種：m為第二接近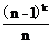

的整數。錯位重排：記n封信的錯位重排數為Dn，則

 

　　n個數的錯位重排數Dn是(n-1)的倍數。

　　8.抽屜原理

　　如果要把n個物件分配到m個容器中，必有至少一個容器容納至少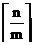

個物件。

　　9.運籌問題

　　物資集中問題：路兩側物資總重量小的流向總重量大的

　　10.濃度問題

　　11.日期問題

　　平年與閏年：每個世紀的前99年，能被4整除的年份為閏年

　　每個世紀的最后一年，能被400整除的年份為閏年

　　平年有52個星期零1天，則每過一年，星期數的變化加1。閏年有52個星期又2天，比平年多出2月29日這一天，所以若經過的某段時間包含2月29日，星期數的變化加2。

　　月歷推斷：

　　結論一：任意星期數的日期呈奇偶交替排列。

　　結論二：每個月任意星期數最少出現4次，最多出現5次。

　　結論三：隻有每月1、2、3日對應的星期數可能出現5次.

　　大月每個月有31天，當月1、2、3日對應的星期數出現5次;

　　小月每個月有30天，當月1、2日對應的星期數出現5次;

　　閏年2月有29天，當月1日對應的星期數出現5次。

　　12.植樹問題

　　閉合路線植樹：棵數=總路長÷間距

　　非閉合路線植樹：棵數=總路長÷間距+1

分享讓更多人看到